数の集合の中から、ある数を探し出すアルゴリズムとして有名なものに、線形探索法と二分探索法と呼ばれるものがあります。
今回は、これら2つのアルゴリズムについて、説明します。
【目次】
1.はじめに
1.1.探索とは
1.2.探索と配列
1.3.今回の探索のプログラムの全体像
2.線形探索法
2.1.線形探索法のアルゴリズム
2.1.1.線形探索法のアルゴリズムのフローチャート
2.2.線形探索法の時間計算量
2.2.1.線形探索法の最大の繰り返し回数
2.2.2.時間計算量の書き方
2.2.3.線形探索法の時間計算量
3.二分探索法
3.1.二分探索法のアルゴリズム
3.1.1.二分探索法のアルゴリズムのフローチャート
3.2.二分探索法の時間計算量
3.2.1.二分探索法の最大の繰り返し回数
3.2.2.二分探索法の時間計算量
4.まとめ
5.おまけ
5.1.おまけ(1)Scratchのリスト(配列)の機能
5.2.おまけ(2)Scratchの繰り返し処理(反復処理)の機能
5.3.おまけ(3)
1.はじめに
これから考える探索のアルゴリズムを考えるのに必要な基本事項を、この「1.はじめに」で整理します。
1.1.探索とは
探索とは、一般的には、ある状況下で、ある特定のものを探すことです。
今回のテーマである線形探索法と二分探索法で扱う探索では、数の集合から、特定のある数を探します。
1.2.探索と配列
プログラムにおいて、個々の変数は、その定義により記憶領域のバラバラな位置に場所が確保され、定義以降そのプログラム内では、定義で命名した変数名によって、変数にアクセス、すなわち、内容を参照したり、変更したりすることができます。
一方、数十万個や数百万個にもなるような数の集合を扱う可能性のあるプログラムを作るとき、1つ1つの数を1つ1つ変数として定義して取り扱うことは非常に大変・・・、というより、定義だけですら、時間がかかり過ぎて、変数で処理するのは現実的でないことがお分かりいただけると思います。
このような場合は、変数の代わりに配列(プログラミング言語によってはリストといいます)を使います。
配列は、記憶領域の中に、変数と同じ大きさの領域が複数連続して並んだものをひとまとめとして扱える変数の集合体で、全体に対して1つの名前を付けて扱います。
連続して並ぶ1つ1つを、配列の要素といい、全体に対して付ける名前を、配列名といいます。
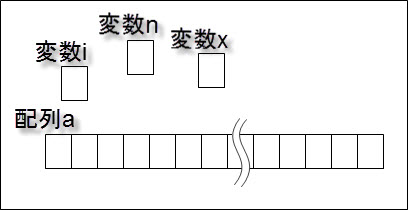
配列の各要素にアクセスするには、配列名と、要素の並び順に割り当てられた番号を使います。
この番号を添字とか、要素番号といいます。
配列の最初の要素の添字は、プログラミング言語によってさまざまで、0から始まるもの、1から始まるもの、プログラマーが定義した任意の数字から始められるものなどがあります。
ちなみに、IT企画研究所のブログ記事でよく取り上げる、子供向けプログラミング言語 Scratch(スクラッチ)では、配列の機能はリストと呼ばれ、添字は1から始まります(要素数がnのとき、配列の添字が1から始まるプログラミング言語の配列の最後の要素の添字はn)。
プログラミング言語の多くは、配列を記憶領域に用意するために、プログラムのはじめに配列名と要素数を宣言して静的に定義し、その要素数の大きさの、その配列名でアクセスできる配列を、記憶領域の適当な場所に確保します。
このことは、言い換えれば、プログラムが実行される前に配列の大きさ(要素数)を決めておく必要があるということです。
そこで、このようなプログラミング言語を使用して、大きな要素数の配列を扱う可能性があるプログラムを作る場合は、大きめの要素数で配列を定義しておきます。
1.3.今回の探索のプログラムの全体像
今回の探索を行うプログラムでは、核となる処理の前に、次のような処理をプログラミングしていると、イメージしていただければと思います。
・任意の数の集合は、配列 aに格納する(配列 aを適当に大きな要素数で定義して場所を確保)
・任意の数の集合の総数n(nは配列 aの最大の要素数より小さい値)と、探したいある数xは、実行時にユーザーに入力させる
・配列 aの各要素は、組み込みのライブラリなどから提供される、乱数を発生する関数などを使って自動生成して代入しておくことにする
プログラムの全体像がつかみにくいと思ったので、核となる部分の前の処理の1例として、上記を書いてみました。
以降、核となる主要部分の処理のアルゴリズムを中心に説明していきます。
では、次の2以降で、探索処理の核となる部分のアルゴリズム、線形探索法と二分探索法の2種類を説明します。
2.線形探索法
2.1.線形探索法のアルゴリズム
線形探索法は単純な探索法です。
次の(1)と(2)がアルゴリズムの概略で、核となる処理です。
(1)探したい数xと、数の集合の配列 aの要素とを、要素の並びの端から1つ1つ順に比較し
(2)探したい数xと等しい要素が配列 aに見つかるまで、次々に隣の要素と比較することを繰り返します。
なお、(1)と(2)の処理で最後の要素まで探して、等しい要素が見つからなかった場合も想定してアルゴリズムは作ることにします。
また、プログラムには、最後に、探した結果を表示するなどの処理を加えます(見つけた場合はその添字を、見つからなかった場合は見つからなかったというコメントを出力・・・、など)
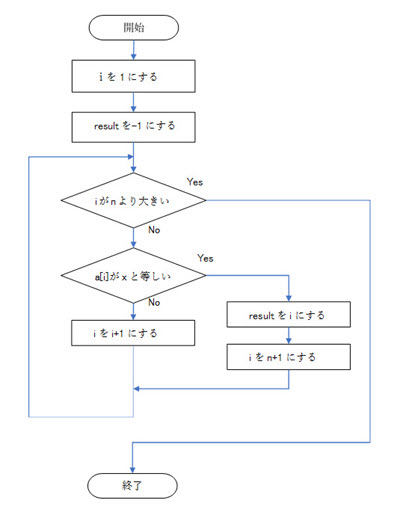
2.1.1.線形探索法のアルゴリズムのフローチャート
今回のフローチャートでは、下記の変数を使い、また、下記の記述方式や条件、方針でアルゴリズムを作りました。
・配列 aの添字 iの要素をa[i]と記述することにします。
・添字は1から始まるものとします(必然的に、最後の要素の添字は、要素数がn個のとき、nとなります)。
・変数 resultを用意して、変数 resultには、探したい数xと等しい値を持つ配列aの要素を見つけたときにはその添字 iを、要素の最後まで調べても見つからなかったら-1を持つように、アルゴリズムを作ります。
・配列 aの各要素に値を用意する処理をこのフローチャートには含めていません。
・探したい数xの入力処理をこのフローチャートには含めていません。
・結果の出力処理をこのフローチャートには含めていません。
・このフローチャートでは、ループ(繰り返し処理)は、前判定を使って記述します。
・このフローチャートでは、ループの条件判定について、偽のとき、ループを繰り返す記述を行います。
・このフローチャートでは、構造化プログラミングを意識し、goto文(無条件のジャンプ)を使わないアルゴリズムにしています。
2.2.線形探索法の時間計算量
2.2.1.線形探索法の最大の繰り返し回数
線形探索法で最も繰り返しの回数が多くなるケースは次の2つです。
・配列の最後の要素(だけ)が、探したい数xと等しい値のとき
・配列のすべての要素が、探したい数xと等しくないとき
これら2つのケースでは、繰り返しの処理がn回行われます。
2.2.2.時間計算量の書き方
あるアルゴリズムの時間計算量は、O記法(オーキホウ、または、オーダーキホウと読みます)と呼ばれる記法で記述します。
取り扱う要素数n(nは十分大きい数と仮定)を処理するとき、Oと()を使い、()の中に、核となる処理の繰り返しの最大の(最悪の)場合の回数を、nを使った式で記述します。
nが十分大きいので、O記法の()の中のnを使った式は、nの定数倍やnの2番目以降の次元の項は、省略します。
具体的には、核となる処理の繰り返しの最大の場合の回数が、nを使った式で、例えば、3nのときは、O記法では3nの定数を省略してO(n)と記述し、3×(nの2乗)+5nのときは、次元の小さい項5nは省略され、さらに、定数3も省略されO(nの2乗)と記述します。
2.2.3.線形探索法の時間計算量
2.2.1.で見たように、線形探索法では核となる処理をn回繰り返すので、線形探索法の時間計算量はO(n)となります。
3.二分探索法
3.1.二分探索法のアルゴリズム
二分探索法は、ソート(並べ替え)された配列を利用して行う、非常に速い探索法です。
探したい数xと、昇順にソートされた要素数nの配列 aがあり、変数 leftにはじめの要素の添字 1を、変数 rightに最後の要素の添字 nを代入し、
(0)left>rightなら、繰り返しを終了します。そうでないなら、a[left]~a[right]の真ん中の要素 a[mid]と探したい数xを比較し、
(1)a[mid]=xなら、探索できたことになり、探索を終了します。
(2)a[mid]>xなら、探したい数xは、あるとすれば元の配列の左半分である、要素 a[left]~a[mid-1]の部分配列にあるはずだから、変数 rightに(mid-1)を代入して(0)の処理に戻ります。
(3)a[mid]<xなら、探したい数xは、あるとすれば元の配列の右半分である、要素 a[mid+1]~a[right]の部分配列にあるはずだから、変数 leftに(mid+1)を代入して(0)の処理に戻ります。
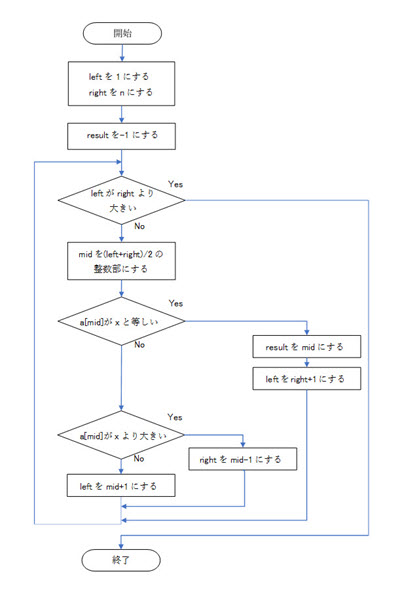
3.1.1.二分探索法のアルゴリズムのフローチャート
今回のフローチャートでは、下記の変数を使い、また、下記の記述方式や条件、方針でアルゴリズムを作りました。
・配列 aの添字 iの要素をa[i]と記述することにします。
・添字は1から始まるものとします(必然的に、最後の要素の添字は、要素数がn個のとき、nとなります)。
・変数 resultを用意して、変数 resultには、探したい数xと等しい値を持つ配列aの要素を見つけたときにはその添字 iを、要素の最後まで調べても見つからなかったら-1を持つように、アルゴリズムを作ります。
・配列 aに対して、調べる要素の並びの範囲を半分に半分に・・・と、これ以上半分にできないところまで変えていくアルゴリズムを書くために、変数 leftと変数 rightを用意して使用します(その範囲の一番小さい添字を変数 leftに、範囲の一番大きい添字を変数 rightに、随時保存)。
・変数 midを用意して、配列 aのど真ん中の要素の添字を随時保存する際に使用します。
・配列 aの各要素に値を用意する処理をこのフローチャートには含めていません。
・探したい数xの入力処理をこのフローチャートには含めていません。
・結果の出力処理をこのフローチャートには含めていません。
・このフローチャートでは、ループ(繰り返し処理)は、前判定を使って記述します。
・このフローチャートでは、ループの条件判定について、偽のとき、ループを繰り返す記述を行います。
・このフローチャートでは、構造化プログラミングを意識し、goto文(無条件のジャンプ)を使わないアルゴリズムにしています。
3.2.二分探索法の時間計算量
3.2.1.二分探索法の最大の繰り返し回数
二分探索法で最も繰り返しの回数が多くなるケースは次の2つです。
・最後の最後に行った比較で、探したい数xを見つけたとき
・配列のすべての要素が、探したい数xと等しくないとき
二分探索法の繰り返しは、オリジナルの配列 aの要素数nの半分(端数切り捨て)の半分(端数切り捨て)・・・で最後に要素1つになるまでの回数なので、逆に考えると、最大の繰り返しの回数は、1の2倍、その2倍、そのまた2倍・・・の計算結果がnをはじめて超えたときまでに2倍した回数と考えることができ、よって、log ₂ n回ということになります。
3.2.2.二分探索法の時間計算量
時間計算量ではnが十分大きい数であることを前提として考えるので、時間計算量を対数で表すとき、対数の底が2でもe(= 2.71828 18284・・・)でも10でも誤差の範囲としてとらえ、通常、計算量としてO記法で書くときは、底なしで表記します。
よって、二分探索法の時間計算量はO(log n)となります。
ただし、これは、ソートの時間計算量を含んでいません。
一般に、データとして保存されている配列は、ソートされていることが多く、二分探索法は、その場合に非常に有効な探索法です。
一方、(ソートにはいろいろなアルゴリズムがあり、あるソートのアルゴリズムについて、他のソートのアルゴリズムと比べると非常に速いアルゴリズムであったとしても)ソートは探索と比べると、かなり長い時間を要す処理です。
なぜなら、ソートは、すべての要素の値を必ず参照し、要素間で値の大小を調べて、必要なら要素間の値を入れ替える処理だからです。
4.まとめ
探索のアルゴリズムの、時間計算量は
・線形探索法⇒O(n)
・二分探索法⇒O(log n)
です。
線形探索法の時間計算量 O(n)が意味する、最大の(最悪の)繰り返しの回数は、すべての要素(n個)に繰り返しアクセスした場合ですので、単純にn回です。
よって、n=100のとき最大の(最悪の)繰り返しの回数は100回、n=10000のときは10000回、n=100000のときは100000回です。
次に、二分探索法の時間計算量 O(log n)が意味する、最大の(最悪の)繰り返しの回数について、例えば、nが100のとき、いくつになるか具体的に求めてみます。
二分探索法では要素数nの配列からはじめて、探索対象の要素を、探したい数が入っている可能性のある半分の要素の集合に絞る処理を繰り返します(半分の要素数から成る配列とみなして新たに同じ処理を繰り返します)。
そのため、逆に2を何回か掛け合わせていく中で、はじめてnを超えたときの回数が、二分探索法の核となる繰り返しの最大の(最悪の)回数です。
二分探索法において、n=100のとき、
2の2乗は4、2の3乗は8、2の4乗は16、2の5乗は32、2の6乗は64、2の7乗は128なので、
よって、n=100のとき最大の(最悪の)繰り返しの回数は7回になります。
同様の方法で検証すると、
二分探索法において、n=10000のとき、
2の8乗は256、2の9乗は512、2の10乗は1024、2の11乗は2048、2の12乗は4096、2の13乗は8192、2の14乗は16384なので、
よってn=10000のとき最大の(最悪の)繰り返しの回数は14回になります。
また、二分探索法において、n=100000のとき、
2の15乗は32768、2の16乗は65536、2の17乗は131072なので、
よってn=100000のとき最大の(最悪の)繰り返しの回数は17回になります。
線形探索法と二分探索法の時間計算量を比較すると、二分探索法の方がとても小さいので、速いことがわかります。
例えば、n=100000のとき、線形探索法の最大最悪の繰り返し回数は100000回に対して、二分探索法の回数は17回なので、その桁の比較だけでも、二分探索法の速さがわかると思います。
ところが、二分探索法における探索では、探索前に行うソート処理にかかる時間計算量も考慮する必要があります。
ソートは探索に比べて時間計算量が大きく、一般にソートの中では効率がよいと言われているクイックソートの時間計算量でも、O(nlog n)です。
したがって、二分探索法を使う際、探索する対象の数の集合を変えずに、新たな探索を続ける場合であれば、2度目の探索以降で数の集合(配列 a)のソートを再度行うことのないよう、プログラミングでは気を付けます。
これには、もう1つ理由があって、二分探索を何度行っても、探索する配列の要素の順序や値に影響を与えることはないため、一度ソートされている配列を再度ソートすることは無意味だからでもあります。
5.おまけ
子供向けプログラミング言語 Scratch(スクラッチ)で、線形探索法と二分探索法の2つの探索処理を同時に含むプログラム(Scratchではプロジェクトといいます)の実行例を、YouTube動画として公開したので、ご覧いただくことができます。
参考:YouTube動画「Scratch2.0:線形探索法と二分探索法のプロジェクトの実行例」
5.1.おまけ(1)Scratchのリスト(配列)の機能
なお、Scratchの配列の機能はリストと呼ばれます。
他の多くのプログラミング言語の配列が実行前に配列の要素数を決めて宣言した大きさで用意され固定される(=静的)のに対して、Scratchのリストは実行時にリストの要素数(長さといいます)を自由に変えることができます(=動的)。
このプロジェクトでも、新しく配列 aの内容を用意し直すときは、一度、すべてのリストの要素をメモリから解放し、要素数を0にしてから、改めてメモリ内に必要な要素数分の領域を取り直す処理をしています(そして、個々の要素には、乱数を発生する組み込みの演算機能で値を用意し直しています)
そのため、桁の大きな要素数を新規に用意し直すのには、長めの時間を要します。
特に、ステージ上に配列の内容を表示したまま、配列を生成し直したり、ソートしたり、探索したりすると、時間がかかるので、動画では、大きな要素数を扱う際、ブロックパレットの配列名の前にあるチェックボックスのチェックを外して、ステージ上の配列の内容の表示を非表示に変えてから操作しています。
5.2.おまけ(2)Scratchの繰り返し処理(反復処理)の機能
Scratchには、ブロックと呼ばれる命令があり、繰り返し処理を行うブロックは3種類用意されています。
このブロックの中で、終了条件に自由な条件を記述できるブロックは1種類で、[制御]グループの[<>まで繰り返す] ブロックです。
この[制御]グループの[<>まで繰り返す] ブロックは、前判定で、記述した終了条件が偽の間繰り返し処理を行います。
5.3.おまけ(3)
IT企画研究所では、子供のプログラミング教育を考える大人をサポートしています。
IT企画研究所のブログでは、Scratchを中心とした子供向けプログラミング言語などに関する情報を大人の皆様に向けてお届けしています。
また、以下のアルゴリズム関連の記事なども公開しています。
・アルゴリズム:再帰:ハノイの塔
・色とRGB値と16進数について|フルカラーの取り扱い:IT基礎
・2進数、10進数、16進数の変換:IT基礎
・アルゴリズムの基本:値の交換…swap(スワップ)…➀
・フローチャートやループの基本|そうだ、アルゴリズムを勉強しよう!

コメント
[…] 情報源: 定番アルゴリズム:線形探索法と二分探索法 […]