はじめてのプログラミング言語を習得しようとしている方からよく寄せられるご要望の1つが、“アルゴリズムを知りたい!”です。
そこで、今回は、プログラミングとの関係、フローチャート(流れ図)の書き方、ループ(繰り返し)、サブルーチンなど、アルゴリズムの基本についてお話しします。
【目次】
1.アルゴリズムとは
1.1.アルゴリズムであるための条件
1.2.アルゴリズムの例
1.3.よいアルゴリズムとは
2.アルゴリズムの3つの基本構造
2.1.順次構造(逐次構造)とは
2.1.1.順次構造(逐次構造)のフローチャート
2.1.2.順次構造(逐次構造)の例
2.1.3.マルチタスクとシングルタスク
2.1.4.順次構造(逐次構造)のまとめ
2.2.選択構造(分岐構造、または、条件構造)とは
2.2.1.選択構造(分岐構造、または、条件構造)のフローチャート
2.2.2.選択構造(分岐構造、または、条件構造)の例
2.2.3.選択構造(分岐構造、または、条件構造)のまとめ
2.3.反復構造(繰り返し構造、ループ)とは
2.3.1.反復構造(繰り返し構造、ループ)のフローチャート
2.3.2.反復構造(繰り返し構造、ループ)の例
2.3.3.反復構造(繰り返し構造、ループ)のまとめ
3.アルゴリズムの表記法
3.1.プログラムの設計図としての表記法
3.1.1.フローチャート(流れ図)
3.1.2.その他
3.1.3.プログラムの設計図としての表記法のまとめ
3.2.プログラミング言語
4.アルゴリズムの基本のまとめ
5.おまけ
5.1.Wordでのフローチャートの書き方
5.2.IT企画研究所のサイトの説明
1.アルゴリズムとは
アルゴリズムは、問題解決の方法を具体的に表した手順のことで、更に、コンピューターで問題解決をするアルゴリズムであるためには、正当性と停止性を満たしている必要があります。
1.1.アルゴリズムであるための条件
手順がコンピューターで問題解決をするアルゴリズムであるための条件は、次の2つを満たしていることです。
・正当性
・停止性
<正当性>
プログラムの正当性とは、与えられた問題に対して正しい解決の結果を出すと保証されることを言います。
めちゃくちゃな結果を出す手順は、正当性を満たしていないため、アルゴリズムとは言えません。
<停止性>
アルゴリズムの停止性とは、どんな入力があった場合でも、有限時間内に必ず正しく停止できることを言います。
例えば、設計やコーディングにおいて、一部の処理の流れを何度か繰り返し行うことを記述しているとき、ちょっとしたミスや勘違いで、永遠に同じ一連の処理の流れを繰り返してしまうような手順(これを、無限ループと言います)を記述してしまうことがあります。
このような手順は、停止性を満たしていないため、アルゴリズムとは言えません。
ここでは正当性と停止性の細かい説明については省略しますが、要は、手順であるだけでなく、正しい結果を出し、どんな入力があったとしても必ず止まるとき、アルゴリズムであると言えます。
1.2.アルゴリズムの例
アルゴリズムは、コンピューターやITの世界に限らず、身近なところでたくさん見かけます。
・家具などの組み立ての説明書
・料理などのレシピ
・家電やコンピューターなどの操作説明書
・「〇〇マニュアル」
例.「お客様対応マニュアル」など
これらのアルゴリズムを表したものは、様々なスタイルやデザインで様々な媒体に自由に作られるものなので、一見同じ目的のものとは思えませんが、すべて何かの手順を表して伝えることを目的として作られたものです。
<ソフトウェアライフサイクルプロセス>
ご存じのように、コンピューターのプログラムで問題解決を行う場合も、その手順を考え出し、書き出す作業があります。
コンピューターのプログラムで問題解決を行う作業の流れは、ソフトウェアライフサイクルプロセス(参考:ソフトウェアライフサイクルプロセスの共通フレーム2007 【 SLCP-JCF2007 】。情報処理推進機構(IPA)が2007年10月に発行したソフトウェア取引に関するガイドライン)と呼ばれます。
1.問題提起
問題が発生して、その解決をプログラムで行うことを決心するまでの過程。
2.要求定義
問題の具体的な洗いだしと、解決として得たい結果をまとめる作業。
3.設計
2の結果を得るための手順、すなわち、アルゴリズムを作る作業。
4.コーディング
3のアルゴリズムをプログラミング言語でプログラミングする作業。
言い換えると、3のアルゴリズムをプログラミング言語の文法に従って書く作業。
5.テスト
4で作ったプログラムをデバッグする作業。
(デバッグとは、エラーや期待しなかった結果を修正して、エラーのない、期待する結果を実現するプログラムにすることを言います)
6.運用・保守
プログラムを現実の問題解決に適用し、必要に応じて、修正などの保守を行う作業。
上記でわかるように、コンピューターのプログラムで問題解決を行う場合には、1つの問題解決に対して、「3.設計」と「4.コーディング」の2回それぞれで、アルゴリズムを記述します。
「3.設計」では、アルゴリズムを考え出してプログラミング言語に依存しない表記法を使って記述し、「4.コーディング」では、「3.設計」で作ったアルゴリズムをプログラミング言語で書き換えて記述します。
すなわち、アルゴリズムを考え出すのは、「3.設計」での作業になります。
なお、この記事の中でのアルゴリズムの記述には、特に断りのないところでは、フローチャート(流れ図とも言います。設計の記述に使用する表記法の1つ)を使用します。
1.3.よいアルゴリズムとは
よいアルゴリズムとは、次のようなアルゴリズムです。
・わかりやすい
・速い
・効率がよい
・再利用しやすい
<わかりやすい>
アルゴリズムは、それを作り利用する自分と、それを利用するすべての人のために、わかりやすいものであることが要求されます。
正当性と停止性を満たした正真正銘のアルゴリズムであっても、難解な作りになっているものも少なくありません。
人にとってのわかりやすさを追求して作ったアルゴリズムは、仮に間違った結果を出すアルゴリズム(間違った結果を出しているので、正当性の要件を満たさず、アルゴリズムとは呼べませんが…)を作ってしまった場合でも発見と修正がしやすく、すぐに修正して正しい“アルゴリズム”にすることができます。
わかりやすいアルゴリズムは、人に説明しやすく、人から理解されやすく、自分自身でも他の人でも再利用する際に使いやすいものとなります。
近年のシステムは、たくさんのプログラムが連動していたり、プログラム自体が大きく複雑なものも多いので、開発には複数の人が関わっていたり、過去に作ったプログラムの一部をそのまま持ってきて再利用したり、修正して利用したりなど、自分の手元を離れて使われることも頻繁にあります。
そのため、特にコンピューターのプログラムで問題解決を行う場合のアルゴリズムでは、わかりやすさが他のすべての要件より優先されます。
当然、わかりやすさを追求すれば、処理速度が少し遅くなったり、処理効率が若干悪くなったりすることもあります。
それらの悪くなり方の度合いにもよりますが、わかりやすさがより向上するのであれば、アルゴリズムを作る際は、基本的にはわかりやすさが最優先されます。
ちなみに、わかりやすいアルゴリズムとは、次のようなアルゴリズムです。
・簡潔
・無理のない自然な流れ
<速い>
コンピューターのプログラムで問題解決を行う場合のアルゴリズムでは、より速く結果を得られるアルゴリズムはよいアルゴリズムと言えます。
ただ、コンピューターなどのハードウェアの性能がとてもよくなっている昨今、特殊な処理以外では、処理速度を上げるアルゴリズムを一番に意識して作ることは少ないようです。
<効率がよい>
コンピューターのプログラムで問題解決を行う場合のアルゴリズムでは、より効率のよいアルゴリズムがよいアルゴリズムと言えます。
ここで言う効率がよいとは、プログラム実行時のメモリの使用量が少ないことを意味します。
昨今のコンピューターでは、ワープロソフトやブラウザソフト、表計算ソフトなどなど、いろいろなソフト(=プログラム)を同時に起動して使用します。
このとき、各プログラムがメモリの一部を使用しています。
そのため、実行時にメモリの多くの部分を使用するプログラムは「効率の悪い」プログラムということになります。
メモリは買い足して大きくすることができますが、少ないメモリの使用で動く「効率のよい」アルゴリズムを考えることは大切です。
メモリをどの程度使用するかは、データの利用の仕方や関数呼び出しなどに関わります(このことについては、別の機会にブログ記事にしたいと思います)。
<再利用しやすい>
<わかりやすい>の項目でも述べたように、コンピューターのプログラムは再利用されることを意識して作成する必要があります。
再利用しやすくするには、よく使われそうな汎用的な手順をまとめて、1つのアルゴリズムとして作成しておくことで対応します。
2.アルゴリズムの3つの基本構造
コンピューターのプログラムで問題解決を行う場合のアルゴリズムは、構造化プログラミングの手法を使って構築します。
構造化プログラミングはエドガー・ダイクストラ(オランダ。情報工学者)らによって1960年代後半に提唱されたプログラミング技法です。
構造化プログラミングは、次の3つの基本構造のみを使って、1つの入り口と1つの出口を持つプログラムを組み立てれば、正当性を検証でき、また、読みやすいものを作ることができるとしていて、現在でも多くのプログラミング言語などがこの技法に対応した機能(構文、命令文、命令語、ブロックなど)をもつなど、基本となる考え方として普及しています。
・順次構造…次に実行される処理は、並べられた順の次に位置する処理となる手順の構造。逐次構造とも言います。
・選択構造…条件を調べる処理があり、その次に実行される処理は、条件を満たした側に用意された処理となる手順の構造。分岐構造とか条件構造とも言います。
・反復構造…一連の処理の流れを繰り返す手順の構造。繰り返し構造とも言います。
2.1.順次構造(逐次構造)とは
順次構造は、順序性がある、処理の並びです。
処理は並んでいる順に実行されます。
このように、順次構造の構造自体はとても単純です。
けれども、順次構造の処理の並びは、他の人が見てもわかりやすいように、問題解決に到達するまでの手順を簡潔な構成、かつ、現実的で自然な順序になるように心がける必要があります。
2.1.1.順次構造(逐次構造)のフローチャート
順次構造は、フローチャートでは長方形と矢印で表します。
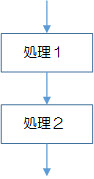
図2-1-1では、[処理1]→[処理2]の順に実行されます。
2.1.2.順次構造(逐次構造)の例
手順の現実的で自然な順序を、今回はショートケーキを作るアルゴリズムで考えてみます。
<ショートケーキを作るアルゴリズム>
1.材料を混ぜて生地を作る
2.生地を焼いてスポンジケーキを作る
3.スポンジケーキが冷めるまで待つ
4.生クリームを泡立てる
5.スポンジケーキに泡立てた生クリームを塗る、飾る
6.苺を飾る
このアルゴリズムで、「6.苺を飾る」処理は、1~5までのすべての処理の実行後に行う必要があります。
例えば、「5.スポンジケーキに泡立てた生クリームを塗る、飾る」前にスポンジケーキに苺を飾ると、生クリームを後でケーキにつけるとしても、苺の下に生クリームがないケーキになってしまいます。
「3.スポンジケーキが冷めるまで待つ」前にスポンジケーキに苺を飾ってしまうと、苺の下に生クリームがないケーキである上に、苺がスポンジケーキの熱で変化してしまう可能性もあります。
また、「2.生地を焼いてスポンジケーキを作る」の前では、生地はドロドロの状態なので、そもそも苺をのせる固ささえありません。
その一方で、「4.生クリームを泡立てる」処理は、「5.スポンジケーキに泡立てた生クリームを塗る、飾る」より前であれば、いつ行っても構いません。
極端な話、生クリームの泡立ては、「1.材料を混ぜて生地を作る」より前でも構いません。
2.1.3.マルチタスクとシングルタスク
現実的なタイミングとしては、焼いたスポンジケーキを冷ましている間に生クリームを泡立てるのが、時間の使い方としても、新鮮な泡立て具合の生クリームをちょうどいいタイミングで利用できることからもベストだと思います。
この同時に2つの処理を行うことを、ITの用語ではマルチタスクと言います。
マルチタスクに対して、一度に1つの処理だけを行うことを、ITの用語ではシングルタスクと言います。
今回はアルゴリズムの基本をお話しするのが目的なので、シングルタスクのアルゴリズムを中心に説明します。
そこで、ショートケーキを作るアルゴリズムも、シングルタスクのアルゴリズムで考えてみます。
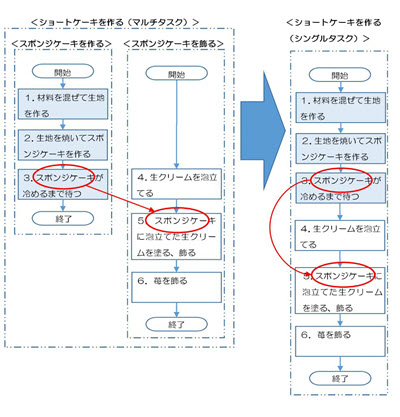
図2-1-2の大きな矢印の右側が、左側の2つのタスク(マルチタスク)の<スポンジケーキを作る>と<スポンジケーキを飾る>を1つのタスク(シングルタスク)にまとめて作ったアルゴリズム<ショートケーキを作る>です。
先の考察で、「4.生クリームを泡立てる」はもっと前に処理されても構わない処理でしたが、この例では「5.スポンジケーキに泡立てた生クリームを塗る、飾る」の直前に置きました。
この理由は、もともと「4.生クリームを泡立てる」が<スポンジケーキを飾る>の処理の1つだったことです。
「4.生クリームを泡立てる」を唐突に流れの最初の処理などとはせずに、自分でも、他人でも、誰が見ても理解しやすい処理の流れにするため、<スポンジケーキを飾る>の一連の処理の1つとしてひと固まりでまとめました。
2.1.4.順次構造(逐次構造)のまとめ
順次構造は、ただ処理を並べるだけなので構造自体を理解し使用することは簡単です。
けれども、処理の並びの順序(手順)は安易に決めることなく、1つ1つよく検討して配置します。
順次構造の部分は構造が平板なため、構造の形から処理の並びの意図を汲み取ることが難しく、それを補足するためには、意図して関連する処理をまとめ、かつ、無理のない自然な順序を心がけて処理を並べます。
2.2.選択構造(分岐構造、または、条件構造)とは
選択構造は、ある時点での条件の結果によって、処理の流れを振り分ける手順です。
選択構造には、2つに分ける単一分岐、単一分岐をいくつか組み合わせて3つ以上に分ける多重分岐などがあります。
なお、分岐した流れは、最終的には1か所に集約するように作る必要があります(構造化プログラミングで言うところの、「1つの出口」にするため)。
2.2.1.選択構造(分岐構造、または、条件構造)のフローチャート
選択構造は、フローチャートでは菱形と矢印で表します。
選択構造では、基本的には1つの選択で2つに分岐させます。
フローチャートでは、選択構造を表記するとき、菱形1つについて、基本的には下1点から1方向と右1点から1方向の計2方向のみに処理を分岐させます。
また、どの条件を満たしたときの矢印なのかがわかるように、図の中には必ず、矢印の線に沿って条件の結果を文字で記入します。
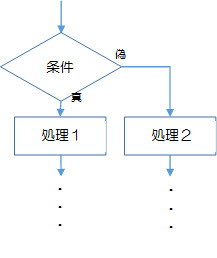
図2-2-1では[条件]の結果が真ならば→[処理1]→…の順で、[条件]が偽ならば→[処理2]→…の順で実行されます。
2.2.2.選択構造(分岐構造、または、条件構造)の例
<選択構造の単一分岐の例1>
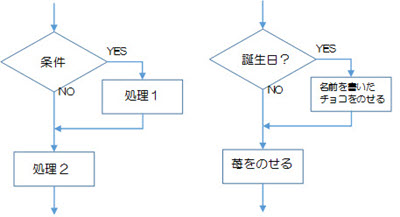
図2-2-2の左の図では、[条件]の結果がNOならば→[処理2]の順で、[条件]の結果がYESならば→[処理1]→[処理2]の順で実行されます。
図2-2-2の右の図では、[誕生日?]の結果がNOならば→[苺をのせる]だけの処理が行われ、[誕生日?]の結果がYESならば→[名前を書いたチョコをのせる]→[苺をのせる]の2つの処理が実行されます。
<選択構造の単一分岐の例2>
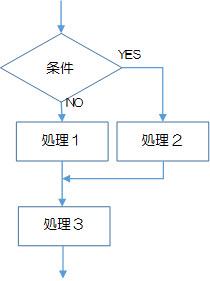
図2-2-3では、[条件]の結果がNOのとき→[処理1]→[処理3]の順で、[条件]の結果がYESのとき→[処理2]→[処理3]の順で実行されます。
<選択構造の多重分岐の例>

図2-2-4では、[条件]の結果が1のとき→[処理1]→[処理4]の順で、[条件]の結果が2のとき→[処理2]→[処理4]の順で、[条件]の結果が1と2以外のとき→[処理3]→[処理4]の順で実行されます。
2.2.3.選択構造(分岐構造、または、条件構造)のまとめ
選択構造は、基本的には処理を一度に2つに分岐させる構造です。
プログラミング言語によっては、一度の選択で一気に多重分岐できる命令語をもつものもあり、その場合には、フローチャートの書き方も少し工夫して、図2-2-4を図2-2-5のように書く書き方もありますが、
<選択構造の多重分岐の例(図2-2-4の書き替え)>
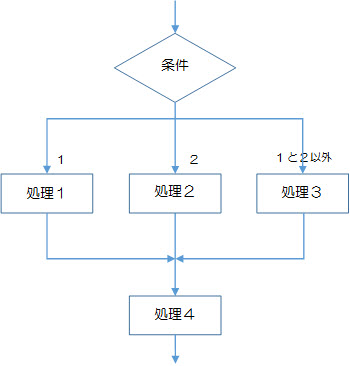
プログラミング言語に依存しないフローチャートにするためには、図2-2-4のように設計します。
なお、選択分岐では、条件で分岐した後の分岐先それぞれの処理の流れを把握しつつ、最終的には1つの流れに集約されるように設計します(構造化プログラミングで言うところの、「1つの出口」にするため)。
2.3.反復構造(繰り返し構造、ループ)とは
反復構造は、一連の処理の流れを繰り返す手順の構造です。
一連の処理の流れを繰り返すかどうかは、毎回判定して決めます。
1回目の一連の処理の流れについて、実行の前に繰り返すかどうかの判定を行うスタイルを前判定と言います。
1回目の一連の処理の流れについて、実行の後に繰り返すかどうかの判定を行うスタイルを後判定と言います。
反復構造がアルゴリズムであるためには、一連の処理の流れの繰り返しは有限回となるように設計します。
プログラミングの用語で繰り返しのことを、ループとも言います。
反復構造の中に反復構造を記述することも可能で、これを多重反復構造とか、多重ループ、ネスト、入れ子などと言うこともあります。
無限に一連の処理の流れを繰り返す構造は無限ループと言い、停止性を満たさない構造なので、アルゴリズムとしては成立しません。
2.3.1.反復構造(繰り返し構造、ループ)のフローチャート
反復構造は、フローチャートでは菱形と長方形と矢印で表します。
反復構造は、フローチャートでは別の記法もあり、六角形2つを使って一連の処理の流れを挟んで表します。
2.3.2.反復構造(繰り返し構造、ループ)の例
<反復構造の前判定の例>
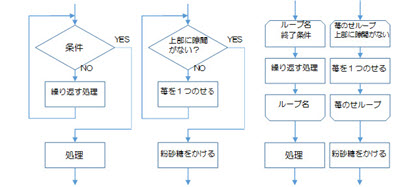
前判定の手順なので、図2-3-1の左から2番目と一番右の図の手順は、初めに隙間がなければ、苺は1つものせることなく、次の粉砂糖をかける処理を行います。
<反復構造の後判定の例>
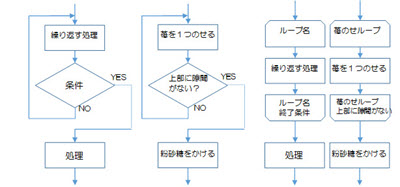
後判定の手順なので、図2-3-2の左から2番目と一番右の図の手順は、初めに(隙間の有無に関係なく)必ず苺を1つのせます。
そのあと、判定をして隙間があれば追加で苺を1つのせる処理を繰り返し、隙間がなくなると繰り返す処理を終了して、次の粉砂糖をかける処理を行います。
<多重反復構造(多重ループ、ネスト、入れ子)の例>
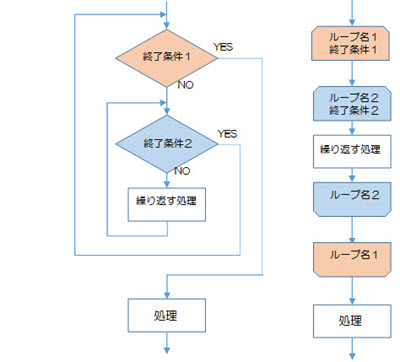
図2-3-3は、同じ2重ループをアルゴリズムの2つの表記方法で書いたものです。
多重反復構造では、ループは他のループ全体を内側に入れることができ、1つのループの始まりから終わりまでの間に、他のループの始まりだけや終わりだけなどの一部だけを入れることはできません。
<無限ループの例>

図2-3-4では、1+2は定数同士の足し算であることから、この条件の結果は永遠に3のため(3以外になることがない)、苺を1つのせる処理を無限に繰り返す手順になってしまいます。
これは無限ループであり、停止性を損なっているため、アルゴリズムとしては破綻しています。
2.3.3.反復構造(繰り返し構造、ループ)のまとめ
反復構造は、一連の処理を繰り返す構造で、この構造を使うと、アルゴリズムを簡潔でわかりやすくまとめることができ、また、処理速度も上がります。
繰り返しの条件の判定をより自然に表す手順を考えるとき、前判定と後判定では、前判定の方が自然であるという場合が圧倒的に多いようです。
フローチャートの六角形の図で表す反復構造では、繰り返しの条件の判定を“(繰り返しを)終了(する)条件”で記入することになっていますが、プログラミング言語によっては、繰り返しの条件の判定を“繰り返しを続ける条件”で記述するものもあるので、アルゴリズムをプログラミング言語に書き替える際は気を付けてください。
最後に余談ですが、ネストとは英語のnestのことで、鳥の巣と言う意味があります。
3.アルゴリズムの表記法
アルゴリズムを表記する記法には、設計段階で利用するものと、プログラミング時に使用するものの大きく分けて2種類があります。
3.1.プログラムの設計図としての表記法
このブログ記事の中でも使用しているフローチャートの他にも、プログラムの設計図を書くための表記法は、実はたくさんあります。
ここでは、まず、フローチャートの基本事項でまだ説明していないことを補足してから、他の表記法も紹介します。
3.1.1.フローチャート(流れ図)
フローチャートは、JIS規格にもなっているアルゴリズムを図で表す記法で、その制定は1970年4月1日、最新改正年月日は1986年2月1日(日本産業標準調査会)と古くからあるものですが、現在でもアルゴリズムの基礎を学習するときに使われる代表的な記法になっているなど、広く普及している記法です。
この記事で説明してきたように、フローチャートでは構造化プログラミングの3つの基本構造を、基本的に矢印、長方形、菱形だけで書くことができます。
また、見た目をシンプルにしてわかりやすくするために、反復構造(繰り返し構造)では更に2種類の六角形を追加して使用することも可能です。
この記事でまだ説明していない、最低限必要なフローチャートの記号は、あと2つあります。
それは、メインルーチンやサブルーチン (モジュール)の定義に使用する端子の記号と、サブルーチン(モジュール)を呼び出す記号です。
<端子>
端子の記号は横長の楕円で、1区切りの手順の始まりと終わりに使います。
<文字列「Hello World」を出力するだけのプログラムの例>
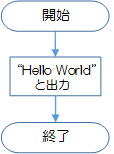
端子は、プログラムの処理の流れの最初の上に付けて「開始」や「START」と記入し、また、最後の下に付けて「終了」や「END」と記入します。
コンピューターのプログラムで問題解決を行うためのアルゴリズムの設計の最終目標は、使用するプログラミング言語の1命令(文、ブロックなど)に1処理が対応する処理の流れの手順を作ることです。
けれども、構造化プログラミングで設計するとき、はじめからプログラミング言語の1命令に1処理が対応するような細かい手順を考えることは行わず、まず、問題解決を、大まかな手順で設計します。
次に、大まかな手順の中のそれぞれの大まかな処理を、更に、少し細かい手順に落とすという作業を繰り返します。
そして、最終的にはプログラミング言語の1命令に1処理が対応するところまで落とします。
ただ、1つのプログラムをプログラミング言語の1命令に1処理が対応するところまで落としてすべて並べると、処理の数が非常に多くなり扱いにくいので(システムによっては命令の総数が数千とか万の位になるものもあります)、細かい手順に落とす途中に、区切りの良いところで処理の流れを分割して、いくつかのまとまりにします。
この1つ1つをモジュールと言います。
端子は、モジュールの始まりと終わりを表すために使用します。
プログラムの始まりと終わりがあるモジュールをメインルーチンと言い、その他をサブルーチンと言います。
メインルーチンの始まりにつける端子には「開始」や「START」、終わりにつける端子には「終了」や「END」と記入します。
サブルーチンには、名前を付け、その名前をサブルーチンの処理の始まりの上につける端子に記入し、終わりの下につける端子には「リターン」や「RETURN」と記入します。
<サブルーチン(呼び出しのための記号)>
処理の流れの途中でサブルーチンを呼び出す記号は、長方形の左右の縦棒が2重になっている図を使用します。
<端子とサブルーチンの例:ショートケーキを作るアルゴリズム2>
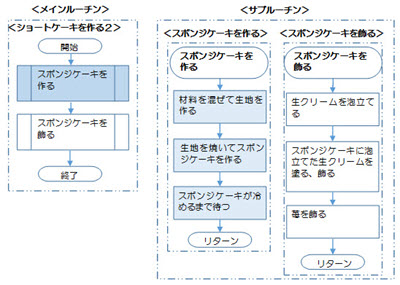
3.1.2.その他
<構造化チャート>
プログラミングの設計図としての表記法では、わかりやすさを追求したフローチャートに代わる構造化プログラミングを表現する表記法として、1970年代ごろからコンピューターメーカーや他国などが考えだした表記法がいくつかあり、それらを総称して構造化チャートと言います。
構造化チャートには、以下のようなものがあります。
| No. | 開発元 | 記法略称 | 記法名称 |
|---|---|---|---|
| 1 | NTT | HCP | Hierarchical and ComPact description chart |
| 2 | 日立 | PAD | Problem Analysis Diagram |
| 3 | 日電 | SPD | Structured Programming Diagram |
| 4 | 富士通 | YAC | Yet Another Control chart |
| 5 | IBM | HIPO | Hierarchy plus Input Process Output |
| 6 | アメリカ | NSチャート | Nassi Shnederman chart(Nassiらによる) |
| 7 | イギリス | DSD | Design Structure Diagrams |
| 8 | ドイツ、オランダ | PSD | Program Structure Diagrams(NSチャートと同じ) |
| 9 | フランス | LCP | Logical Conception of Program flow chart |
1980年代後半に、私も仕事でPADを使用していたことがあります。
PADは、とても使いやすく読みやすい表記法で、今でも自分用の資料を作る際に使用することがあります。
一方、その頃アメリカ系企業のSEだった友人は、NSチャートを使用していたそうです。
これら構造化チャートの記法は、デファクトスタンダード(事実上の標準)であったフローチャートの改良版としてそれぞれ開発された記法で、それぞれがとても使い勝手の良い特徴を持っています。
けれども、残念ながら、企業など特定の集団にそれぞれの記法の使用者が固定化されたまま、一般にはあまり広まらなかったので、構造化プログラミングにおけるデファクトスタンダードの表記法はフローチャートのまま、現在に至ります。
参考サイト:Acroquest プログラミング講座
https://www.acroquest.co.jp/webworkshop/programing_course/note.html
参考サイト:JISC 日本工業標準調査会 https://www.jisc.go.jp/
規格番号JISX0128 規格名称プログラム構成要素及びその表記法
<UML>
UMLはUnified Modeling Languageの略で、日本語では統一モデリング言語と言い、プログラムやシステムの状態や動きを表すいくつかの図の体系を持った図式言語です。
HP、IBM、サン・マイクロシステムズなどによって1989年に結成されたOMG(Object Management Group)という非営利の標準化コンソーシアムが、オブジェクト指向システムにおける様々な表記法を統一する目的で開発し、1997年にバージョン1.0を発表しました。
OMGのサイトhttps://www.omg.org/spec/UML によると2015年6月にバージョン2.5がリリースされているところまで、現時点で確認できます。
オブジェクト指向では、フローチャートで表現しきれない概念がいくつもあり、オブジェクト指向開発の黎明期には多くのオブジェクト指向開発方法論と表記法が提唱されました。
表記法が乱立したため、業界標準となるものが必要とされ、オブジェクト指向開発方法論者のJames E, Rumbaugh、Grandy Booch、Ivar Jacobsonの3人が中心となって、彼らやその他の方法論をまとめる形でUMLを開発しました。
UMLの仕様は大きく、持っている図は10を超えます。
図はざっくり分類すると構造図と振る舞い図の2種類に分けられます。
UMLの図の中で、フローチャートと比較的近いのは、振る舞い図の中のアクティビティ図と呼ばれる図の記法です。
参考サイト:Object Management Group サイト https://www.omg.org/spec/UML
参考サイト:Wikipedia … Object Management Group
https://ja.wikipedia.org/wiki/Object_Management_Group
3.1.3.プログラムの設計図としての表記法のまとめ
現在ではオブジェクト指向や並列処理(マルチタスクを実現する処理)のプログラムやシステムが多いため、最終的にはUMLなどを利用できるようになることが望まれます。
それでも、アルゴリズム学習の第1歩は、資料や説明書が数多くあり、構造化プログラミングの表記法としてデファクトスタンダードになっている、フローチャートから始めることをお勧めします。
フローチャートと構造化プログラミングの手法は、UMLを学習する際、アクティビティ図の理解などに知識として利用できます。
3.2.プログラミング言語
プログラミング言語もアルゴリズムを表記するものの1つです。
4.アルゴリズムの基本のまとめ
以上、今回はアルゴリズムの基本を、フローチャートと構造化プログラミングの手法を中心に説明しました。
5.おまけ
5.1.Wordでのフローチャートの書き方
YouTubeのIT企画研究所代表のYukari Nishimuraチャンネルから、以下の動画「Wordでのフローチャートの書き方」を公開しています。
お時間があれば、ご参考までに、是非リンクをクリックして動画をご覧ください。
5.2.IT企画研究所のサイトの説明
IT企画研究所では、子供のプログラミング教育を考える大人をサポートしています。
IT企画研究所のブログでは、Scratchを中心とした子供向けプログラミング言語などに関する情報を大人の皆様に向けてお届けしています。
以下のアルゴリズム関連の記事なども公開しています。
・アルゴリズム:再帰:ハノイの塔
・定番アルゴリズム:線形探索法と二分探索法
・色とRGB値と16進数について|フルカラーの取り扱い:IT基礎
・2進数、10進数、16進数の変換:IT基礎
・アルゴリズムの基本:値の交換…swap(スワップ)…➀
また、IT企画研究所サイト更新情報を、月2回のメール配信でお知らせしています。
メール配信の登録は無料です。

コメント
[…] フローチャートやループの基本|そうだ、アルゴリズムを勉強しよう! […]