ハノイの塔の再帰のアルゴリズムを説明します。

目次
１．ハノイの塔とは
 ２．再帰とハノイの塔
 ２．１．再帰
 ２．２．ハノイの塔
 ３．検証：回数の計算
 ４．おまけ

１．ハノイの塔とは

ハノイの塔とは、次の条件で円板を動かす解法を考えるゲームです。
（１）3本の柱があります
（それぞれAの柱、Bの柱、Cの柱と呼ぶことにします）
（２）Aの柱に大きさの異なる円板がn個重なってはまっています
（一番大きい円板が一番下、上に向かって徐々に円板の大きさは小さいものになるように積まれています）
（３）Aの柱のn個の円板を、Cの柱を作業用に使って、Bの柱に移動します
（４）円板は、1度に１つずつ動かします
（５）作業のいかなるときでも、大きい円板の上に小さい円板を重ねます
（小さい円板の上に大きい円板を乗せてはなりません）

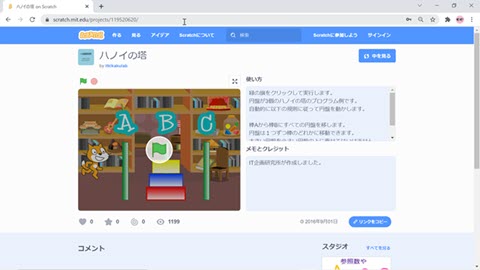
こちらのリンクは、n=3のハノイの塔の円板の動きをグラフィカルに表現しているScratchのプロジェクトページ（下図）です。
ご興味のある方は、ご参考までにリンクをクリックしてプロジェクトページを表示し、緑の旗のマークをクリックして実行してみてください。

２．再帰とハノイの塔

２．１．再帰

一般に、ある関数の定義の中で、その関数自身を呼び出すことを再帰と言います。

２．２．ハノイの塔

再帰を使うと、ハノイの塔を比較的簡単にプログラミングすることができます。
そのため、ハノイの塔は再帰を学習する際の題材としてよく使われます。

ハノイの塔を、再帰を使ってどう処理していくかを、考えていきます。
とりあえず、ここでは関数の表現を、「関数名（引数1、引数2、･･･）」という形で記述していきます。

これから作ろうとするハノイの塔の関数で、引数として、円板の数n、円板がある柱a、円板を移動したい柱b、円板の移動の作業用の柱cの4つを用意します。

ハノイの塔（n、a、b、c）

今、nがNのとき、N個の円板をAの柱からBの柱に移すとき、すなわち、ハノイの塔（N、A、B、C）を考えます。

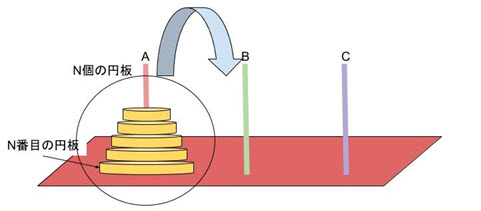
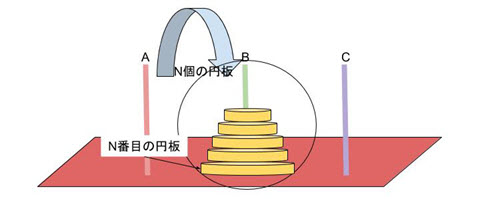
Aの柱の一番下にあるN番目に大きい円板をBの柱にはめるときに注目して考えると、この円板を動かせるときとは、その上にあるすべての円板、すなわち、(n-1)個の円板の山が、Cの柱に移動した直後です（➀）。

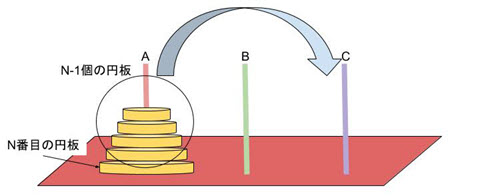
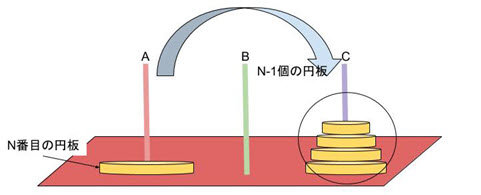
Aの柱にあるN番目に大きい円板をAの柱からはずしBの柱にはめたら（➁）、

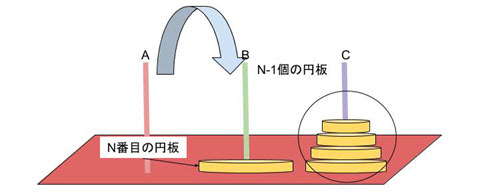
最後に、Cの柱にある（n-1）個の円板の山をBの柱に移動して（➂）ハノイの塔（N、A、B、C）が完了します。

ということで、関数ハノイの塔（N、A、B、C）は、次のようになります。

➀ハノイの塔（N-1、A、C、B）
➁N番目の円板を、Aの柱からはずして、Bの柱にはめる
➂ハノイの塔（N-1、C、B、A）

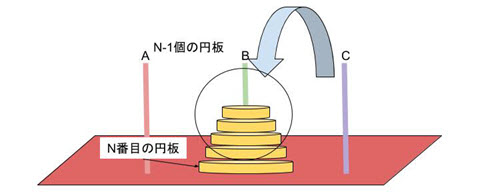
➀では、Aの柱にはまっているN番目に大きい円板1つを残して、その上の（N-1）個の円板の山をCの柱に移します。
このとき、Bの柱は作業用に利用します。
➁では、Aの柱にあるN番目に大きい円板の上には何も乗っていないので、また、Bの柱には円板はないので、ただ、AからBに移してはめます。
➂では、Cの柱によけておいた（N-1）個の円板の山をＢの柱に移します。
このとき、Aの柱は作業用に利用します。

ところで、➀ハノイの塔（N-1、A、C、B）ですが、Aの柱からCの柱にBの柱を作業用に使って（N-1）個の円板の山を移すことを示します。
・Aの柱のにはまっているN番目と（N-1）番目に大きい2つの円板を残して、その上の（N-2）個の円板の山をCの柱移します。
このとき、Cの柱は作業用に利用します。
・Aの柱にある（N-1）番目に大きい円板の上には何も乗っていないので、また、Cの柱には円板はないので、ただ、Aの柱からはずし、Cの柱に移してはめます。
・Bの柱によけておいて（N－2）個の円板の山をＣの柱に移します。
このとき、Ａの柱は作業用に利用します。

すなわち、ハノイの塔（N-1、A、C、B）では、
➀’ハノイの塔（N-2、A、B、C）
➁’（N-1）番目の円板を、Aの柱からはずして、Cの柱にはめる
➂’ハノイの塔（N-2、B、C、A）
を行います。
（N-3）個以下についても同様です。

再帰で処理を考えるときに大事なことは、再帰をやめるポイントを考えることです。
ハノイの塔の場合は、nが0になったら、処理を何も行いません（再帰をやめます）。

すなわち、ハノイの塔（1、A、B、C）では、
➀’’ハノイの塔（0、A、B、C）→何もしない
➁’’1番目の円板を、Aの柱からはずして、Bの柱にはめる
➂’’ハノイの塔（0、B、C、A）→何もしない
となるので、結果的に➁’’の操作しかしないことになります。

この関数のアルゴリズムを図で表すと、以下のようにあっさりした形になります。

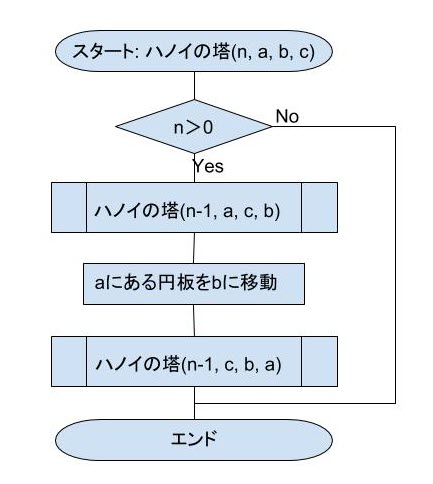
３．検証：回数の計算

次に、何回円板を移動するかをnを使って計算してみます。
n個の円板を動かす回数を $a_n$ で表すとき、アルゴリズムを見て分かる通り、
$$a_n=a_{n-1}+1+a_{n-1}$$
よって、整理して次の漸化式を導くことができます。
$$a_n=2a_{n-1}+1･･･➀$$

n=1のとき、動かす回数は1回なので、$a_1=1$ 。
この初期条件を使って、先の漸化式➀を解きます。
➀は➀’のように変形できます。
$$a_{n}+1=2(a_{n-1}+1)･･･➀’$$
➀’は数列$a_{n}+1=1$ は、初稿が$a_1=2$、公比が$2$の等比数列です。
そこで
$$a_{n}+1=2^n$$
より、したがって、n個の円板を動かす回数$a_{n}$は、
$$a_{n}=2^n-1$$
回となります。

例えば、n=5のとき、31回、n=8のとき、255回円板を動かすことになります。
再帰を使ったこの方法では、最短の動かし方になります。

ところで、このハノイの塔は、フランスの数学者 $\acute{E}douard Lucas$ による創作のお話しです。
その内容は、
＊＊＊＊
宇宙が出来上がったときに、インドの神様の梵天が作った梵天の塔という名の塔があります。
その塔には、3本のダイヤモンドでできた柱（Aの柱、Bの柱、Cの柱とします）と、純金でできた大きさがすべて異なる円板が64枚ありました。
初めに64枚の円板は、すべてが1本の柱（Aの柱）に刺さっていました。
そのとき、一番大きな円板が一番下で、徐々に小さい円版が上に積まれていました。
その塔に勤める僧侶たちは、1度に1つずつ円板を動かし、必ず、大きい円板の上にそれより小さい円板を乗せるルールを守りながら、別の柱（Bの柱）に、大きい円板が一番下、上に向かって徐々に小さいものが乗る形にすべての円板を移すために、昼夜を問わず働いていますが、なかなか完成しません。
完成したときには、世界の終わりが来ると言われいます。
＊＊＊＊

このお話しを計算して検証してみます。
例えば、円板1つを他の柱に移す作業を1秒で行うとした場合、64枚の円板をAの柱からBの柱に移す回数がそれにかかる秒数と同じになります。
最適な方法で動かしたとしても、その秒数は、
$$2^{64}-1=18446744073709551615$$
秒です。
これは約5845億年という計算になり、宇宙がビッグバンから現在までに約137億年経過したことから考えても、確かに、世界の終わりが来るかもしれないくらい、時間がかかる作業ということがわかります。

このセクションの最後に、前半でご紹介したプログラムをScratch2.0で実行した動画「Scratch2.0：ハノイの塔の実行例（再帰など）」をYouTubeで公開しているので、ご紹介します。
よろしかったらリンクをクリックしてご覧ください。

４．おまけ

IT企画研究所では、子供のプログラミング教育を考える大人をサポートしています。

IT企画研究所のブログでは、Scratchを中心とした子供向けプログラミング言語などに関する情報を大人の皆様に向けてお届けしています。

アルゴリズム：再帰：ハノイの塔